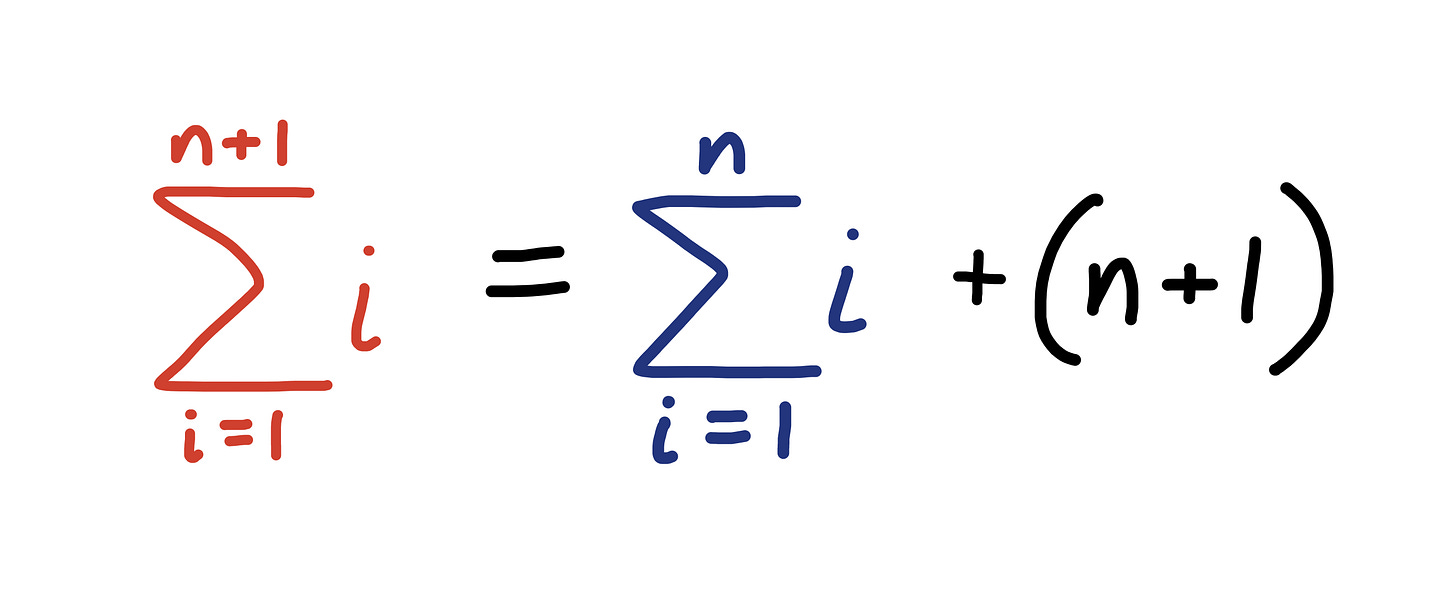I think everyone, even if they don’t care about math, should understand proofs.
Most math concepts are dismissed as impractical. Truthfully, it’s not like anyone is stopped from driving to work unless they can solve a triple integral.
But anyone can benefit from knowing why something is true. That’s what a proof does. It shows us why something is true. In math, a claim is incomplete without its proof.
Proofs come in different breeds:
Direct Proof
Proof by Contradiction
Proof by Counter-example
…And so on.
One type is proof by induction. A proof by induction is powerful, and it’s used often, but it’s also counter-intuitive.
To understand it, we need an infinitely-long ladder.
The Infinite Ladder
Imagine you bought a ladder to space. The ladder has an infinite number of rungs. It was very hard to fit the ladder through the door of the hardware store on the way out.
Obviously you can’t climb the infinite ladder all the way up. Eventually, your muscles would give out. But if that wasn’t a problem, could you climb the ladder?
Well, you can’t climb the ladder if it’s floating 30 feet off the ground.1 You also can’t climb the ladder if some rungs are broken or missing.
You can climb the ladder if these two rules are true:
Rule 1: You can climb onto the 1st rung of the ladder.
Rule 2: No matter which rung you’re on, you can always climb to the next rung on the ladder.
If those two rules are true, here’s a proof that you can climb the ladder:
By rule 1, you can get onto the 1st rung of the ladder.
By rule 2, if you can get to the 1st rung, you can then climb to the 2nd rung.
By rule 2 again, if you can get to the 2nd rung, you can then climb to the 3rd rung.
And so on and so on: you can always climb to the next rung on the ladder by rule 2, so you must be able to climb the ladder all the way to the top.
That’s the basic idea of proof by induction.
Rule 1 proves you can get onto the ladder in the first place. This is called the base case. The base case fails if the ladder is floating in mid-air, for example. If you can’t get onto the 1st rung, you can’t climb the ladder all the way up.
Rule 2 proves that wherever you are on the ladder, you can always climb one rung higher. It’s not about specifically showing that you can get from the 1st rung to the 2nd rung, or from the 15th rung to the 16th rung. It’s about showing that in general, you can get from the nth rung to the (n+1)th rung of the ladder, for some natural number n, regardless of n’s actual value. This is called the induction step. The induction step fails if the 5th rung on the ladder is missing, for example.
Put these two rules together, and you have a proof by induction.
Proof by Induction (Math Example)
There’s a famous story, basically a fable, about the mathematician Carl Gauss. When Gauss was a kid, his teacher made him add up all the integers from 1 to 100. The teacher thought this would take a long time to finish, but shockingly, Gauss quickly found the answer: 5050.
The young Gauss had discovered an equation to sum the first n natural numbers2:
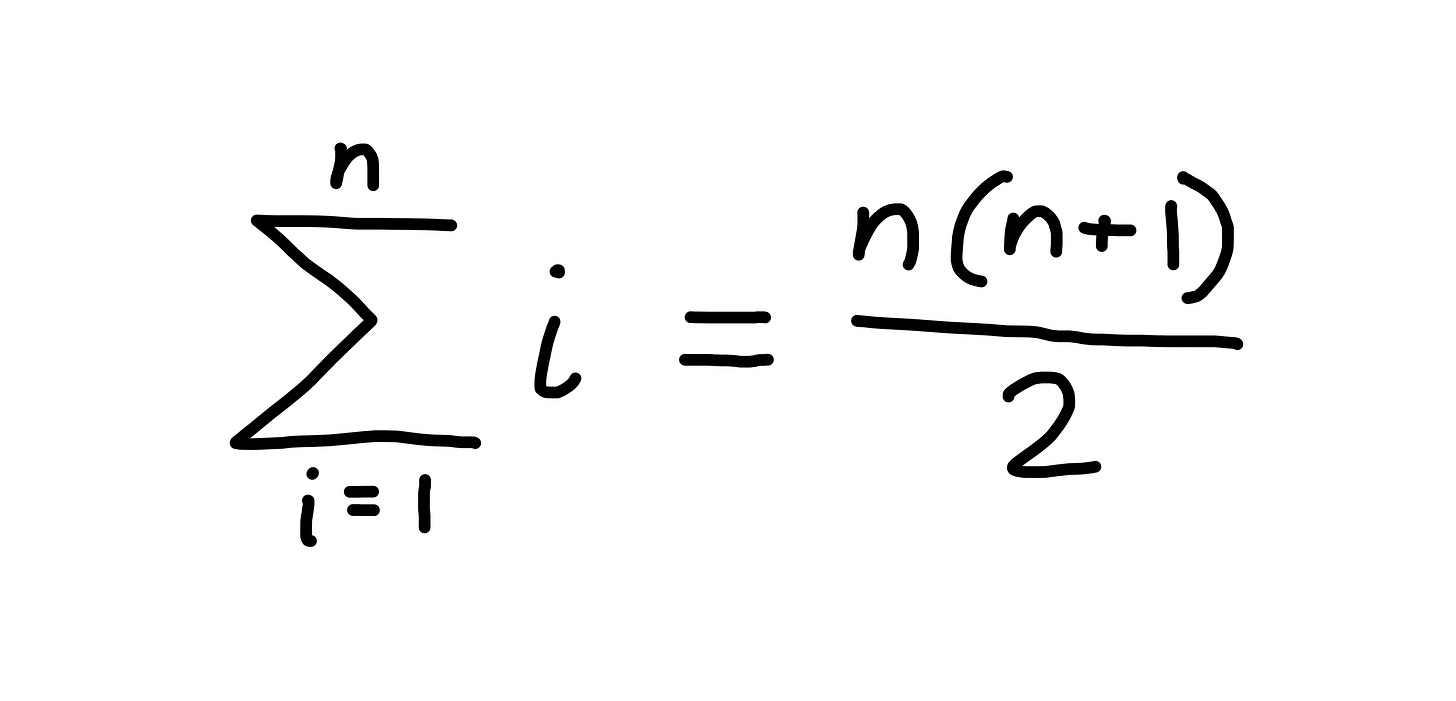
Of course, we don’t have time to manually check if Gauss’s equation is true for every number. But we can prove Gauss’s rule is true with a proof by induction.
Start by proving Rule 1, the base case. To prove the base case, we manually check that both sides of the equation equal each other when n=1. Why 1? Because that’s the first natural number3 (the first rung of the ladder). When n=1, the left-hand-side of the equation is 1. And the right-hand-side of the equation gives us 1(1+1)/2=1. The two sides equal each other, so our base case is true.
Now we have to prove Rule 2, the induction step. This is trickier because it’s more general. We have to prove that if we assume Gauss’s sum is true for the first n natural numbers, then that implies Gauss’s sum is also true for the first (n+1) natural numbers.
For me, it’s helpful to write down exactly what I’m assuming and what I’m trying to prove:
The part you assume is often called the induction hypothesis.
Now we have to show that if Gauss’s sum is true for the first n numbers, then the sum is also true for the first (n+1) numbers.
The sum of the first (n+1) numbers equals (1+2+3+4+…+n)+(n+1). In other words, the sum of the first (n+1) numbers is just the sum of the first n numbers plus (n+1).
But because of our induction hypothesis, we assume the sum of the first n integers equals n(n+1)/2. So we can rewrite our equation like this:
Rearranging the right-hand side with a bit of algebra, we get this:
And that completes our induction step. We have now shown that if Gauss’s sum is true for the first n integers, then it must also be true for the first (n+1) integers.
We showed Rule 1 and Rule 2 are both true, which means Gauss’s sum must be true for every natural number. Our proof by induction is complete.
The Two Steps to Complete a Proof by Induction
Say you’re trying to prove some statement S(n) for all natural numbers, where n refers to a natural number.
There are two steps to prove the statement by induction:
Show that the base case is true. Directly show that either S(0) or S(1) is true, depending on your definition of natural numbers.
Show that “S(n) is true” implies “S(n+1) is true.” Show that if you can get to the nth rung on the ladder, then you can climb to the (n+1)th rung on the ladder, for some arbitrary number n. This is the induction step.
Statement where Base Case Fails but Induction Step is True
I want to make this clear: you need both rules for a proof by induction to work. Let’s look at a statement where Rule 2 (induction step) is true but Rule 1 (base case) is false.
This would be like if your ladder was 30 feet off the ground, but with all its rungs intact. It’s true that if you could get onto some rung of the ladder, then you could get to the next rung. But you can’t get onto the ladder. So you can’t climb the ladder all the way up.
Take a look at this (false) statement:
False Claim: for any natural number n, the sum of every natural number less than or equal to n is (n(n+1)/2)+73
This statement is wrong. The sum of natural numbers up to n, as we went over earlier, equals n(n+1)/2, not (n(n+1)/2)+73. But the induction step still works. Here’s how.
Assume that the statement is true for some natural number n. In other words, Σn = (n(n+1)/2)+73. Then we can show the following:
So Rule 2 (the induction step) is true for this statement.
But if you actually plug in a number for n, like 1, you can see this statement is false. For example, set n=1. The left-hand-side of the equation is the sum of natural numbers up to 1, which is just 1. But the right-hand-side of the equation is (1(1+1)/2)+73, which equals 74, which is a little far off from 1.
Even though the induction step is true for this statement, the base case is false. So our statement is false.
Don’t ignore the base case! It still matters in a proof by induction.
Statement where Induction Step Fails but Base Case is True
You could also have a case where Rule 1 (base case) is true but Rule 2 (induction step) is false. This would be like if your ladder had its 1st rung intact, but all other rungs broken. You can climb onto the ladder, yes. But you can’t climb to the next rung. Mathematically, S(1) might be true, but S(n) → S(n+1) would still be false.
Let’s look at another false claim:
False Claim: for any natural number n, the sum of every natural number less than or equal to n is 1*n.
Our base case will be n=1. The sum of natural numbers up to 1 is 1. Likewise, if n=1, then 1*n=1. So our base case is true.
But it’s easy to see that the statement is false if n equals anything other than 1. If n=2, the sum of natural numbers up to 2 is 3, but 1*n equals 2. That’s a counterexample to the statement, which is enough to disprove it.
Just because a statement is true for some particular number doesn’t make it true for every number.
Proof Beyond All Doubt
Math proofs should be air-tight. That’s the goal.
With Gauss’s sum, it’s tempting to verify the first 6 or 7 cases manually, throw your hands up, and say “Well, it’s probably true for the rest of the numbers.”
That’s not enough for math. We need to know it’s true for the rest of the numbers.
In a court case, you must prove the defendant’s guilt “beyond all reasonable doubt.” But in math, you must also prove a statement is true beyond all unreasonable doubt.
There’s an unsolved math problem called The Collatz Conjecture. It basically says that if you plug a natural number into a specific algorithm, the output will always be 1. The Collatz Conjecture has been manually checked for at least the first 5 quintillion natural numbers (a quintillion is a billion billions). But it’s still considered unsolved.
Why is it still unsolved? Because we can’t prove the Collatz Conjecture is true for every natural number. If you climb the first five-quintillion rungs of a ladder, that doesn’t prove you can climb to rung number five-quintillion-and-one.
You never know, that rung could be broken.
You might reply, “But I could get up onto it with a trampoline! Or a vaulting pole! Or with another, smaller ladder,” but I’m going to assume you can’t afford any of those things because you spent all your money on an infinitely-long ladder.
The story probably isn’t true (For one thing, how did the teacher know the correct answer? Did he also waste his time summing the first 100 numbers the long way?). I like this article by Brian Hayes where he tries to track down where the fable started.
Technically, the natural numbers can start at either 0 or 1. It doesn’t matter which one you pick, as long as you clarify which number you chose. In this case, Gauss’s sum is true regardless of which number you choose.