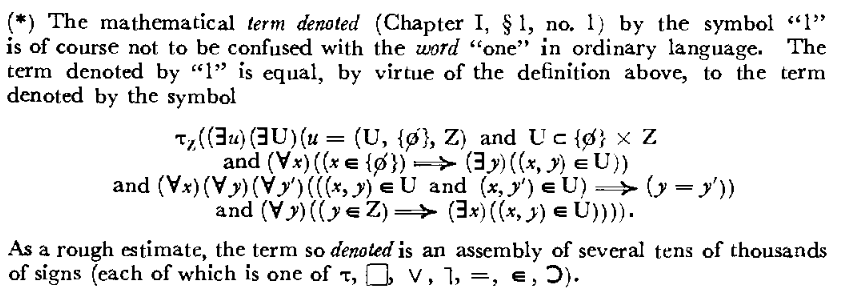How Nicolas Bourbaki Defined the Number 1

Using... 2,409,875,496,393,137,472,149,767,527,877,436,912,979,508,338,752,092,897 symbols

Image by me

I don’t know what the hell is going on.

My goal has always been to make math accessible and digestible, not arcane and esoteric, which probably makes Bourbaki my mortal enemy.

Deep in a foreign land called “France,” there’s a group of mathematicians who anonymously publish math textbooks under the name Nicolas Bourbaki. They were founded in the 1930s, and their goal is to make math extremely precise.

Saying their books are dense is an understatement. Their books might as well have their own gravitational pull. The books are extremely theoretical, which is impressive on one hand, and mind-bogglingly confusing on the other.

Bourbaki defined the number 1 like this:

τZ ((∃u)(∃U)(u = (U, {∅},Z) and U ⊂ {∅} × Z and (∀x)((x ∈ {∅}) =⇒ (∃y)((x, y) ∈ U)) and (∀x)(∀y)(∀y 0 )(((x, y) ∈ U and (x, y 0 ) ∈ U) =⇒ (y = y 0 )) and (∀y)((y ∈ Z) =⇒ (∃x)((x, y) ∈ U)))).

I was going to make a post detailing how this definition works, but truthfully, I don’t fully get it. I gave up on that idea.

What I can do instead is answer a few basic questions:

1. What was Bourbaki’s deal?

2. Why would you ever make the definition of 1 so heckin’ complicated?

3. Did Bourbaki have a point?

It all starts with math’s secret society.

The Secret Society

On December 10th, 1934, six mathematicians met in the Capelaude cafe in a distant city called “Paris.” They ate cabbage soup, grilled meats, braised envides, and pommes souffles (puffy French fries),¹ which sounds delicious.

Their goal was to write a calculus textbook. The best calculus textbook in all of France.

World War I wiped away an entire generation of French mathematicians. By the 1930s, math in France had become outdated. While there were still brilliant French mathematicians (Weil, Chevalley, etc.), many believed France had lost its status as the top country for math. That title now belonged to Germany, with prominent mathematicians like Klein (of bottle fame), Hausdorff (of space fame), and Hilbert (of hotel fame), among many others.

In France, calculus (which at the time was called analysis) was mainly taught with a textbook called Cours d’Analyse Mathematique Vol. 1, published in 1904 by Edouard Goursat. I don’t know how else to say this, but Goursat just looks like a guy who knows he wrote Cours d’Analyse Mathematique Vol. 1:

He’s probably hiding differential equations inside that mustache.

Andre Weil and Henri Cartan, then professors at University of Strasbourg, had problems with Goursat’s book. It was repetitive—a theorem would appear, then reappear with Goursat’s version of the theorem, then reappear with another mathematician’s version, and so on. More importantly, there was a lot of hand-waving. Theorems would appear with a laundry list of assumptions and hypotheses you had to accept before you could actually use the theorem. As though you had to make mathematical leaps of faith just to use anything from the book. This mislead some students into thinking math had little rigor.

Weil and Cartan decided to solve these problems by writing a new analysis textbook. Word spread to other mathematicians in the area, and the group met at Capelaude. They arranged meeting after meeting. Members joined and left. And over time, the goal of the group grew.

Writing a book on analysis wouldn’t be enough. They had to redo all of mathematics with unrelenting precision. They resolved to write a massive tome called Elements de Mathematique, which would be split into 6 volumes:

I. Theory of Sets
II. Algebra
III. General Topology
IV. Functions of a Real Variable
V. Topological Vector Spaces
VI. Integration

The volumes would be published collectively under the alias Nicolas Bourbaki.

Members would stay until they were 50, at which point they had to retire. Every decision the group made had to be unanimous. Meetings consisted of reading a draft line by line, where any member at any time could speak up, ask questions, or object. There was no “president.” Meetings were anarchic. Armand Borel described Bourbaki meetings as “Two or three monologues shouted at top voice, seemingly independently of one another” and Jean Dieudonné compared the meetings to “gatherings of madmen.”

It seems miraculous that Bourbaki could finish even a single book this way. But Bourbaki published the first chapter of their first book, Theory of Sets, in 1939. And Bourbaki has continued to publish, in total, 28 books, the most recent of which was published in 2019 (and a new book set to be published in January 2023).

The Bourbaki Way

Bourbaki’s writing is cold, austere, and extremely technical. Very little guidance is given to the reader. It’s hard to find examples, or descriptions, or motivations for concepts throughout their books.

Bourbaki’s writing style is best explained through comparison. Let’s look at Theory of Sets, by Bourbaki, and a modern set theory textbook, Set Theory: A First Course by Daniel W. Cunningham.

Set theory, broadly speaking, is a branch of math that studies sets. A set is a collection of objects. The real numbers are a set. The numbers {1,2,9,10} are a set. The hats in your hat collection are a set.²

This is how Cunningham introduces set theory:

And this is how Bourbaki introduces set theory:

By the way, Bourbaki’s paragraph comes at the start of the second chapter, after 50-or-so pages explaining what’s meant by “relational signs,” “substantific signs,” “weight,” “schemes,” “explicit axioms,” “letters,” “constants,” and more.

Notice Bourbaki’s paragraph doesn’t include a single word on what a “set” actually is. You know how both Cunningham and I defined a set as a collection of objects? A couple paragraphs further into Theory of Sets, Bourbaki comments on that definition:

In other words: we’re not even going to bother with the definition of “set” as a collection of objects, because we think it’s unnecessary.

Cunningham’s description starts with an “informal description of a set.” He gives an example of a set, and an intuitive description of sets. But Bourbaki’s description is more interested in the logic of the theory surrounding sets. Cunningham’s paragraph is about the “set” part of set theory whereas Bourbaki’s paragraph is about the “theory” part of set theory.

Formal mathematics

The first chapter of Theory of Sets is exclusively about a new, rigorous language for writing about math. Bourbaki calls this language “formal mathematics,” but I’m going to call it “Bourbakian.”

Here’s how Bourbaki begins to describe their language:

It’s easy to miss in the sea of symbols, but we already have two footnotes.

In other words, every mathematical theory utilizes certain symbols. Some symbols are universal, other symbols are specific to each theory. In set theory’s case, the theory employs the specific symbols =, ⊂, and ∈.

Bourbaki then says you can combine symbols one after another to create an assembly. Symbols in an assembly can be linked together with links. This is an example they give of an assembly:

The bars above the symbols are “links.” The τ, ∨, ¬, and ☐ are all “logical signs.” The A’ and A’’ are “letters.” And ∈ is a specific symbol in set theory.

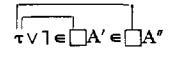
Of course, printing these assemblies throughout an entire textbook would be impractical. Naturally, you start creating shorthand for specific assemblies so you don’t have to write them over and over again. Bourbaki calls these terms and definitions.

Think of it this way: computers operate in binary code, long sequences of 0’s and 1’s. Even something as simple as an upper-case “A” is represented as 01000001. If I want to print a string of text to the console, it would be absurd for me to write a sequence of thousands of 0’s and 1’s. Instead, we bundle specific sequences into functions. I can just write print() as a shortcut for a specific sequence of 0’s and 1’s. A Bourbakian "assembly" is akin to binary code,³ and mathematical definitions are akin to functions in a high-level coding language.

But importantly, Bourbaki says definitions do not belong to formal mathematics. Definitions, they say, lead to confusion because they can be imprecise.

So even though Bourbaki prints, for example, the symbol ∅ for the empty set, the symbol ∅ is shorthand for a very, very long “assembly” of signs (=, ⊂, ∈, τ, ∨, ¬, ☐), links, and letters from “Bourbakian.”

The Number 1

So remember: if you’re writing something in Bourbakian, you are writing an assembly, a long list of symbols and letters. But we turn some of these assemblies into definitions to make life easier.

On page 158 of Theory of Sets, this footnote appears:

Note that there are symbols in that definition like ∃, ∅, ∀, and even 0 that aren’t part of “Bourbakian.” All these symbols are shorthand, and if you wrote them out as their assemblies, they’d be much longer. The definition of 1, printed above, is not the same as the assembly that represents “1.” Bourbaki guesstimates that this assembly is tens of thousands of symbols long.

In 1999, A.R.D. Mathias published this article where he calculated the true number of symbols in the assembly as 4,523,659,424,929. Mathias also points out that a slightly different definition of 1 appears in the 1970 version of Theory of Sets. He states that Robert M. Solovay calculated the number of symbols in the 1970 version as 2,409,875,496,393,137,472,149,767,527,877,436,912,979,508,338,752,092,897, approximately 2.4 * 10^54.

Then in 2010, Jose Grimm calculated the number of symbols at approximately 1.6*10^55, even larger than in Solovay’s calculation. Grimm’s number is close to the number of atoms in our solar system.

Of course, you do not need to write the number 1 with this many symbols. You can just write 1.

Does Bourbaki Have a Point?

If you showed Bourbaki’s work to laypeople uninterested in math, it’s likely that 20% of them would vomit, 30% would scream in terror and run away, and 50% would rant about how math is overly complicated.⁴

Obviously, a definition of 1 with more symbols than there are atoms on Earth is ridiculous. But Bourbaki were still influential throughout the world.

Here are a few impacts Bourbaki has made:

• Bourbaki influenced many mathematicians in Europe throughout the 1950s. Since the 1950s, numerous textbooks have been published with a more Bourbakian style.

• Some Bourbaki books, like the book on Commutative Algebra, are still considered good resources at the graduate level.

• Bourbaki inspired the “new math” method of education that was briefly popular in the States in the 1960s. “New math” was widely considered a failure and was criticized by Richard Feynman among others.

• Bourbaki gave us the notation of Ø for the empty set, which we still use today. So that’s pretty cool.

• For some reason there’s a Twenty One Pilots song named after Nicolas Bourbaki.

Bourbaki also got plenty of criticism, then and now. Mandelbrot didn’t like Bourbaki. V.I. Arnold was strongly against Bourbaki’s influence in Europe. Dieudonné later regretted that the group’s attitude had contributed to an air of snobbery around math in France. Virtually no one teaches with Bourbaki textbooks at the high school or undergraduate levels anymore.

These days, Bourbaki’s books should be read for historical curiosity. You probably shouldn’t read them to learn math. I think it’s impressive how ambitious “formal mathematics” was for its time (they essentially made computer assembly language but for math, and before computer assembly language was invented). But learning math by learning formal mathematics first is like learning to code by learning binary first. It’s not a practical or sensical way to learn. There are plenty of books, videos, and handsome bloggers that are better resources for learning math.

We start with intuition, and crystallize it as rigor. We don’t learn the other way around. Theory is the conclusion of practice.

While rigor is important, it’s not the start point or end point of all math. Terence Tao’s blog post on rigor, while not explicitly about Bourbaki, brilliantly sums up the importance of mathematical rigor:

The point of rigour is not to destroy all intuition; instead, it should be used to destroy bad intuition while clarifying and elevating good intuition. It is only with a combination of both rigorous formalism and good intuition that one can tackle complex mathematical problems; one needs the former to correctly deal with the fine details, and the latter to correctly deal with the big picture.

Tao’s paragraph, notably, is well under 10 thousand symbols long.

1. Source: “A Parisian Cafe and Ten Proto-Bourbaki Meetings 1934-1935", Liliane Beaulieu, from Mathematical Intelligencer 15 no.1 (1993)

2. Including the Big Hat.

3. Or, of course, assembly language.

4. Hypothesis not tested.